What is an Ideal Transformer? Circuit, Working & Phasor Diagram

Electrical Technology

Ideal Transformer and Practical Transformer

Table of Contents

Ideal Transformer

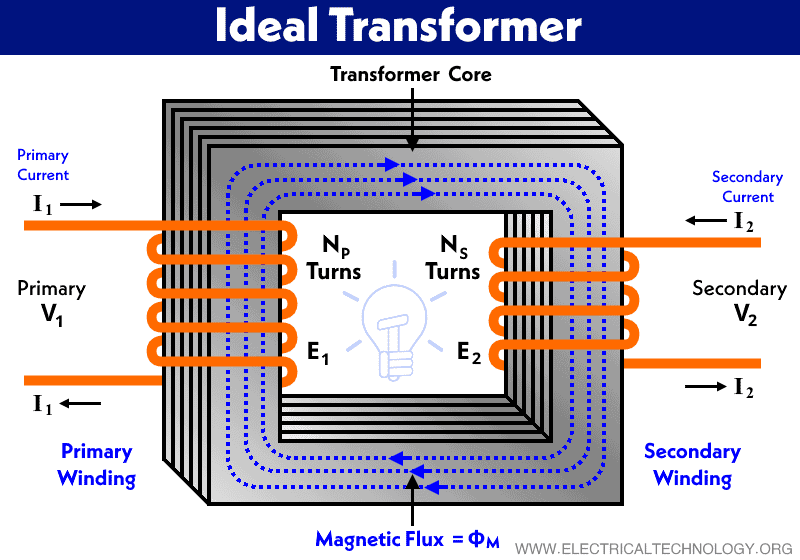
An ideal transformer is an imaginary transformer with zero ohmic, magnetic leakage, copper and core losses. In other words, an ideal transformer is a theoretical transformer (conceptual model) which consists of two pure loss free inductive windings on the core of the transformer. In simple words, the input of an ideal transformer is equal to the output of the transformer. Keep in mind that an ideal transformer is not possible in real life at all.

The practical transformers are designed to have properties close to the ideal transformer. The properties of an ideal transformer are listed below.

The winding resistance (primary and secondary winding resistance) is zero.
Its leakage flux and leakage inductance are zero. Hence, the entire flux is available in the core and link in both windings.
The core permeability is infinite. Therefore, negligible MMF is required to set up the flux in the core.
The losses occurred due to resistance, hysteresis, and eddy current being zero.

Mathematically in an Ideal Transformer,

P_IN = P_OUT

And

V_IN = V_OUT

Similarly

I_IN = I_OUT

Moreover, there are zero losses in an ideal transformer e.g.

Ohmic (Resistive losses = 0
Leakage flux losses = 0
Copper & Core losses = 0

This shows that in an ideal transformer, the input current and voltage on the primary side is equal to the output current and voltage on the secondary side. This way, the overall input electric power to the transformer is equal to the output power of the transformer e.g. the input kVA rating of the transformer is equal to the output kVA rating of the transformer due to no leakage flux, impedance and reactances losses in both of windings of the ideal transformer.

Working of an Ideal Transformer

in an ideal transformer as shown in the figure below, electric current passing through the primary coil creates a magnetic field. The primary and secondary coils are wrapped around a core of very high magnetic permeability, such as iron, so that most of the magnetic flux passes through both the primary and secondary coils. If a load is connected to the secondary winding, the load current and voltage will be in the directions indicated, given the primary current and voltage in the directions indicated (each will be alternating current in practice as a transformer won’t work on DC supply).

The properties of an ideal transformer are not exactly equal to the practical transformer as there are many types of losses that occur in a transformer. It is impossible to get all the above properties in a practical transformer. But we try to achieve properties of practical transformers near to the above properties.

The efficiency of an ideal transformer is 100% as the I²R loss and core loss of the transformer are zero. But in practical transformer, there are some losses that cannot be neglected. And hence, we cannot achieve 100% efficiency in a practical transformer.

The schematic diagram of the ideal iron-core transformer is shown in the figure below.

Here, two coils are wound in the common magnetic core. The coil that is connected with the supply voltage V₁ is a primary winding and the coil that is connected with the load Z_L is a secondary winding.

As we have discussed in the properties of an ideal transformer that there are zero impedances in both windings. Therefore, the voltage induced in the primary winding is equal to the applied voltage V₁. Similarly, the voltage induced in secondary winding E₂ is the same as the secondary voltage V₂.

To produce the required MMF and mutual flux Ф_M, the supply current I₁ is sufficient. This MMF is enough to overcome the demagnetizing effect of the secondary MMF as a result of load.

According to Lenz’s law, E₁ is equal and opposite to V₁.

E₁ = –V₁

The primary and secondary EMF is induced by the same mutual flux. Therefore, the E₁ and E₂ are in the same direction and opposite to the direction of V₁.

The magnetizing current I_μ produces mutual flux Ф_M in phase. And I_μ lags V₁ by 90˚. E₁ and E₂ are produced by mutual flux Ф_M and lags by 90˚. The secondary voltage V₂ is equal in magnitude to E₂ and is opposite to primary voltage V₁.

The below figure shows the phasor diagram of an ideal transformer.

The transformation ratio (turns ratio) (a) for an ideal transformer is defined as below equations.

Where,

a = Transformation ratio
T₁, T₂ = Number of turns in primary and secondary winding
E₁, E₂ = Induced EMF
V₁ = Supply voltage (primary voltage)
V₂= Secondary Voltage
I₁, I₂ = Current passes through the primary and secondary winding

From the above equation,

I₁T₁ = I₂T₂

According to the above equation, we can say that the demagnetizing ampere-turns (AT) of the secondary winding are equal and opposite to the magnetizing MMF of a primary winding of an ideal transformer.

E₁I₁ = E₂I₂

S₁ = S₂

According to the above equation, the apparent power (volt-amperes) drawn from the primary supply is equal to the apparent power transferred to the secondary without any loss in the ideal transformer.

In other words; the input apparent power is equal to the output apparent power.

Input Apparent Power = Output Apparent Power

Therefore, the KVA input of an ideal transformer is equal to the KVA output. This is not happening in the case of the practical transformer as there are some losses.

Practical Transformer

An ideal transformer is explained with some assumptions. These assumptions are not valid for the practical transformer. Because, in an ideal transformer, we have assumed windings with zero resistance and core has infinite permeability. This is not possible as all windings have resistance and core material is not available with infinite permeability.

Therefore, in a practical transformer, we need to consider the winding resistance and leakage reactance.

Winding Resistance

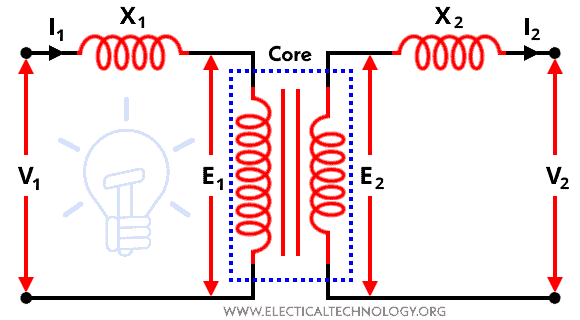
In a practical or actual transformer, there is always some resistance in the primary and secondary winding. The effect of winging resistance considers by adding resistance in series with each winding. The equivalent circuit of the transformer after adding resistance is shown in the figure below.

As the resistance is added to the circuit, there are some amounts of voltage drop that occur in the circuit. Therefore, the induced EMF in the windings is not the same as the voltage. So, we cannot assume secondary terminal voltage V₂ is equal to E₂ and supply voltage V₁ is equal to E₁.

The secondary terminal voltage V₂ is less than the secondary induced EMF E₂ by an amount of secondary voltage drop I₂R₂.

V₂ = E₂ – I₂R₂

Similarly, primary induced EMF E₁ is equal to the vector difference of supply voltage V₁ and primary voltage drop I₁R₁.

E₁ = V₁ – I₁R₁

Leakage Reactance

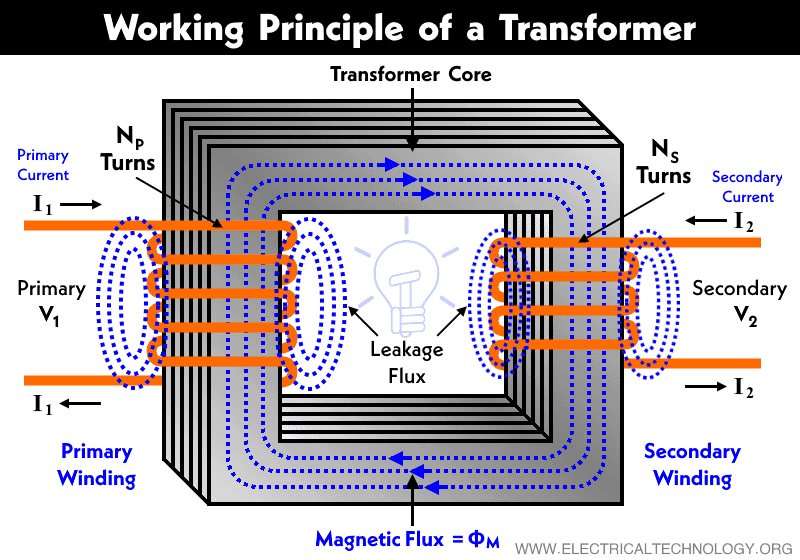
For an ideal transformer, we have assumed that the flux produced by the primary winding links both the primary and secondary windings. But in the case of the actual transformer, not all produced flux is available in the magnetic core. There are some amounts of flux diverted to the non-ferromagnetic material surrounding medium. And also, the core has finite permeability. So, this small amount of flux that flows in the external path is known as primary leakage flux. It is denoted by Ф_L1.

The secondary current I₂ produces a flux Ф₂ that opposes the main flux Ф_M. A portion of this is flux is diverted to the surrounding medium. This leakage flux is called secondary leakage flux Ф_L2. The remaining flux only links the secondary turns and induces EMF E_L2 in the secondary winding.

Therefore, the flux that passes completely through the core and links both windings is called mutual flux Ф_M. The typical diagram of fluxes in a transformer is shown in the figure below.

Due to the leakage flux Ф_L1 and Ф_L2, the induced EMF E_L1 and E_L2 are different from induced EMF E₁ and E₂ caused by the mutual flux Ф_M. The effect of leakage flux is considered by adding an inductance in series with each winding. It is added in such a way that, the voltage drops in each series inductances (X₁ and X₂) are equal to that produced by the leakage fluxes. The representation of leakage reactance is shown in the figure below.